Question

How do you use rotation of axes to identify and sketch the curve of `97x^2+192xy+153y^2=225`?

Answer 1

The curve is an ellipse and after rotation it is `9x^2+y^2=9`

Explanation:

A conic equation of the type of `Ax^2+Bxy+Cy^2+Dx+Ey+F=0` is rotated by an angle `theta`, to form a new Cartesian plane with coordinates `(x',y')`, if `theta` is appropriately chosen, we can have a new equation without term `xy` i.e. of standard form.
![http://philschatz.com/precalculus-book/contents/m49441.html]()
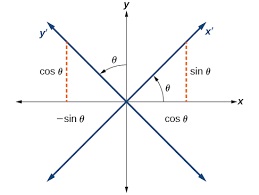
The relation between coordinates `(x,y)` and `(x'.y')` can be expressed as
`x=x'costheta-y'sintheta` and `y=x'sintheta+y'costheta`

or `x'=xcostheta+ysintheta` and `y=-xsintheta+ycostheta`

for this we need to have `theta` given by `cot2theta=(A-C)/B`

In the given case as equation is `97x^2+192xy+153y^2-225=0`, we have `A-C=-56` and `B=192` and hence `cot2theta=-7/24` i.e. `(cot^2theta-1)/(2cottheta)=-7/24` or `12cot^2theta+7cottheta-12=0` or `(4cottheta-3)(3cottheta+4)=0` i.e. `cottheta=3/4` or `cottheta=-4/3`.

We consider only acute angle i.e. `cottheta=3/4`, which leads to `costheta=3/5` and `sintheta=4/5`

Hence relation is give by `x=3/5x'-4/5y'` and `y=4/5x'+3/5y'`

Hence, we get `97((3x')/5-(4y')/5)^2+192((3x')/5-(4y')/5)((4x')/5+(3y')/5)+153((4x')/5+(3y')/5)^2-225=0`

or `97((9x'^2)/25+(16y'^2)/25-(24x'y')/25)+192((12x'^2)/25-(12y'^2)/25-(7x'y')/25)+153((16x'^2)/25+(9y'^2)/25+(24x'y')/25)-225=0`

or `225x'^2+25y'^2-225=0` or `9x'^2+1y'^2=9`

The two graphs are as follows:
graph{97x^2+192xy+153y^2-225=0 [-10, 10, -5, 5]}
and
graph{9x^2+y^2=9 [-10, 10, -5, 5]}