Question

Three towns (A,B, and C) are located so that B is 25 km from A and C is 34 km from A. If <ABC is 110 degrees, how do you calculate the distance from B to C?

Answer 1

`x=(34sin (70 - sin^-1((25sin110)/34)))/sin110`

Explanation:

First, let's draw the triangle in question using all the given.

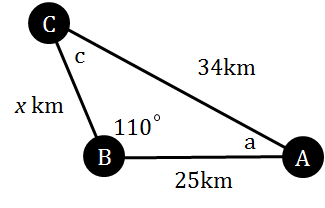
In this diagram, `a` and `c` are angles, and `x` is a side length.

By the Law of Sines, we know that:

`sin a/x = sin110/34 = sinc/25`

We can immediately solve for `c`.

`sin110/34 = sinc/25`

`(25sin110)/34=sinc`

`c=sin^-1((25sin110)/34)`

The sum of angles in a triangle is `180`, so we can solve for a:

`180 = a + 110 + sin^-1((25sin110)/34)`

`a = 70 - sin^-1((25sin110)/34)`

We now just need to solve the following equation for `x`:

`sin (70 - sin^-1((25sin110)/34))/x = sin110/34`

`(34sin (70 - sin^-1((25sin110)/34)))/sin110 = x`

None of the angles or values used are "standard" values on the unit circle, so this is the final answer.