An interesting example is "H"-"C"-="C"-"H"H−C≡C−H, acetylene.
We utilize the convention that the zz axis points along the internuclear axis. Since the pp orbital that overlaps head-on with the ss orbital is along the internuclear axis, the 2p_z2pz orbital of carbon will the one that is compatible with the 1s1s of hydrogen AND the 2s2s of carbon.
)
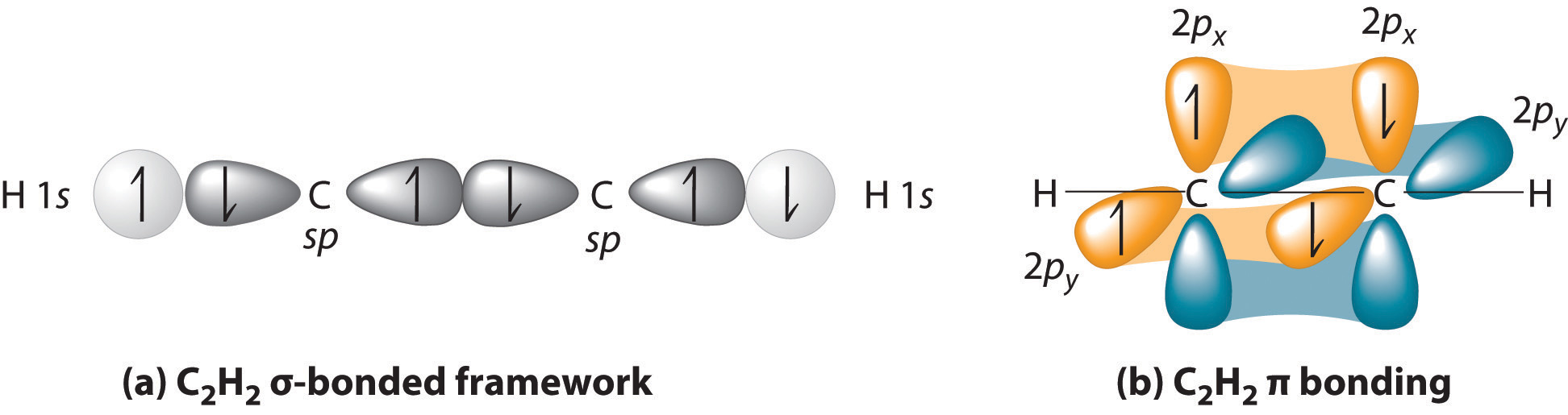
The two carbons each have \mathbf(sp)sp hybridization, where they mix their 2s2s and 2p_z2pz orbitals together, achieving an \mathbf(sp)sp hybrid orbital of 50%50% ss character and 50%50% pp character, with a new, lower energy, between those of the two original atomic orbitals. This can overlap with hydrogen's 1s1s orbital.
That accounts for each ** \mathbf(sigma) bond that each carbon makes with the other carbon and one of the hydrogens; see (a)**.
Then, the remaining 2p_x and 2p_y orbitals of each carbon can respectively overlap with the 2p_x and 2p_y orbitals of the other carbon (i.e. 2p_y with 2p_y). These CANNOT overlap with hydrogen's 1s orbital.
These account for the two \mathbf(pi) bonds; see (b).
Overall, we get that each carbon uses two sp hybrid orbitals by mixing the 2s + 2p_z orbitals in order to overlap with hydrogen's 1s orbital and form a \mathbf(sigma) bond with one of the hydrogens and the other carbon, and each carbon uses its 2p_x and 2p_y orbitals to generate two \mathbf(pi) bonds with the other carbon.
The two \mathbf(pi) bonds and one \mathbf(sigma) bond made by each carbon with the other carbon accounts for the triple bond.
