What are the all the solutions between 0 and 2π for #sin2x-1=0#?
2 Answers
Explanation:
Restricted to
Explanation:
First, isolate the sine
Now, take a look at your unit circle
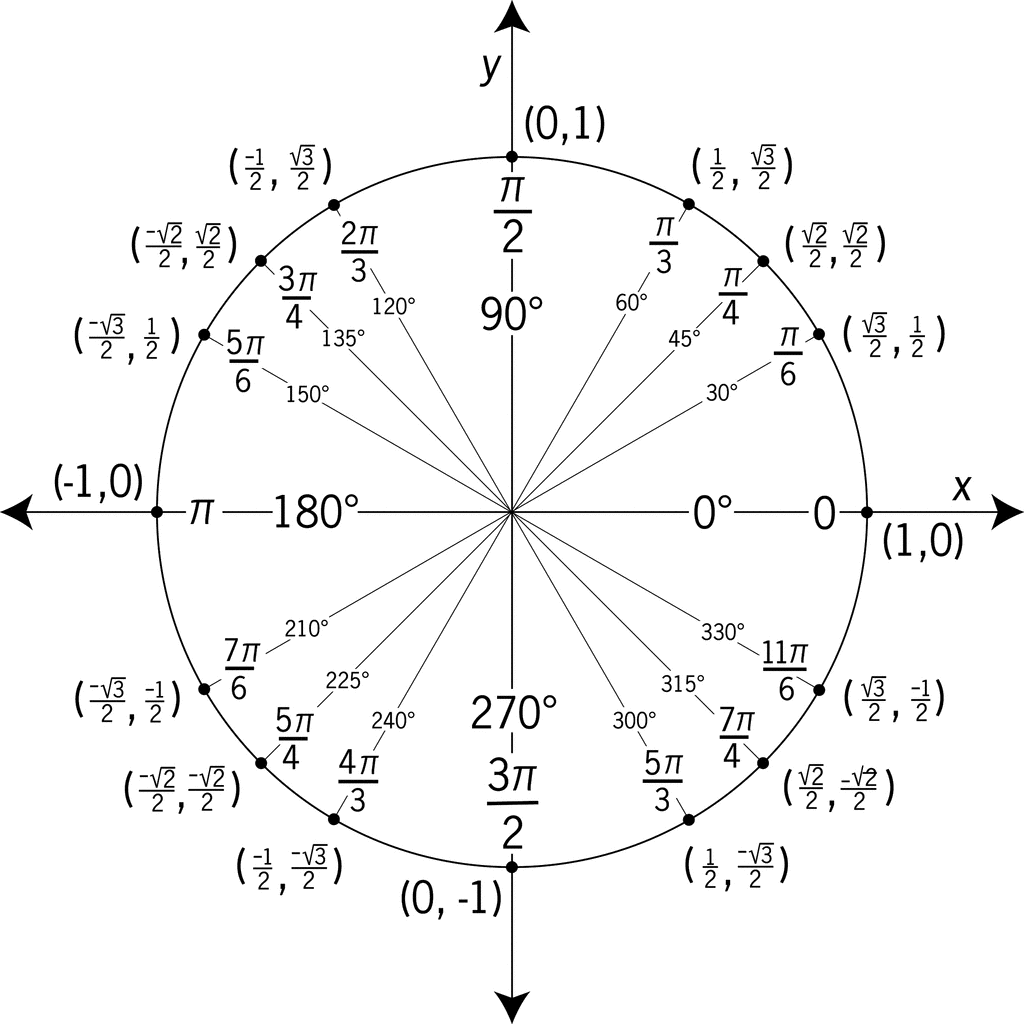
Now, the sine correspond to the
We want to solve for x, so
However, remember that the period of the normal sine wave is
And since



