Question

What are the different kinds of f orbitals?

Answer 1

`f` orbitals are very complex and difficult to describe with words.

Explanation:

So there is only one kind of `f` orbitals and that is the `f` orbital. I suppose you mean the different shapes of the `f` orbitals.

So the `f` orbitals have 7 different shapes (since `n=4` and `l=3` resulting in: `-3, -2, -1, 0, 1, 2, 3`) These structures can be seen in this picture:

![)

With the different dimensions. Hope it helps.

Answer 2

They are quite complicated, and can often do combinations of `sigma`, `pi`, `delta`, and even `phi` bonding.

For an introduction into these kinds of bonds:


`sigma` bonds are in every chemical bond. `pi` bonds start showing up in double and triple bonds (e.g. `"O"_2`, `"N"_2`, etc), `delta` bonds start showing up in quadruple bonds (see link), and `phi` bonds aren't seen until a sextuple bond is made (e.g. in `"Mo"_2` or `"W"_2`).

---

The `4f` orbitals can be separated into three types (here, we use the convention that outer atoms point their `y` axes inwards and `z` axes upwards):

`1)` Two lobes - `sigma` bonding only (`m_l = 0`)

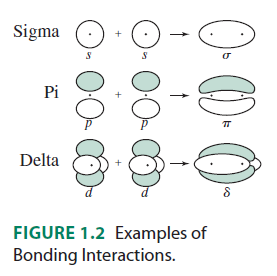
• The `f_(z^3)` (`m_l = 0`) is the only one that only `sigma` bonds. It can bond head-on along the `z` axis.

`2)` Six lobes - `sigma` and `pi` bonding, OR `phi` bonding only (`m_l = -3, +3, -1, +1`)

• The `f_(y(3x^2 - y^2))` (`m_l = -3`) can `sigma` bond along the `x` axes (for example, with a `p_y` orbital) AND `pi` bond along the `y` axes (for example, with a `p_x` orbital, or a `d_(xy)` orbital).

It can alternatively form a `phi` bond (a six-lobed side-on overlap) along the `xy` plane (with another `f_(y(3x^2 - y^2))` orbital in a bimetallic complex).

• The `f_(x(x^2 - 3y^2))` (`m_l = +3`) can `sigma` bond along the `y` axes (for example, with a `p_y` orbital) AND `pi` bond along the `x` axes (for example, with a `p_x` orbital, or a `d_(xy)` orbital).

It can alternatively form a `phi` bond (a six-lobed side-on overlap) along the `xy` plane (with another `f_(x(x^2 - 3y^2))` orbital in a bimetallic complex).

• The `f_(yz^2)` (`m_l = -1`) can form decent `sigma` bonds along the `y` axes, AND/OR `pi` bonds along the `y` AND `z` axes.

It can alternatively form a `phi` bond (a six-lobed side-on overlap) along the `yz` plane (with another `f_(yz^2)` orbital in a bimetallic complex).

• The `f_(xz^2)` (`m_l = +1`) can form decent `sigma` bonds along the `x` axes, AND/OR `pi` bonds along the `x` AND `z` axes.

It can alternatively form a `phi` bond (a six-lobed side-on overlap) along the `xz` plane (with another `f_(xz^2)` orbital in a bimetallic complex).

`3)` Eight lobes - `pi` bonding OR `delta` bonding (`m_l = -2, +2`)

• The `f_(z(x^2 - y^2))` (`m_l = -2`) is for `pi` bonding along ANY of the axes, `x,y`, or `z`. The lobes lie above and below each of the axes, but also along them.

It can alternatively form a `delta` bond with another `f_(z(x^2 - y^2))` orbital in a bimetallic complex.

• The `f_(xyz)` (`m_l = +2`) is for `delta` bonding along ANY of the planes (`xz, yz, xy`) (for example, with `d_(xy)`, `d_(xz)`, or `d_(yz)` orbitals).

It can alternatively form a `pi` bond with another `f_(xyz)` orbital in a bimetallic complex.