Question

How do you find the critical points to graph `f(x) = 4 sin(x -pi/2 )`?

Answer 1

`(pi/2,0)`, `(pi,4)`, `((3pi)/2,0)`, `(2pi,-4)`, `((5pi)/2,0)`

Explanation:

By the five-point method, you need five points to graph the function, `f(x)=4sin(x-pi/2)`. To find the five points, first find the five points for its parent function `e(x)=sinx`. Ignore the negative x values and its corresponding y values in the table below.

![)

Now that you have the five points for the parent function, use the mapping rule to apply transformations in order to find the five points for the transformed function, `f(x)=4sin(x-pi/2)`.

Mapping rule: `(x+color(red)(pi/2),color(blue)4y)`

`f(x)=4sin(x-pi/2)`
Point `1. (0+color(red)(pi/2), color(white)(xxx)(color(blue)4)0) rArr color(white)(xxxxxxxxx)(pi/2,0)`
Point `2. (pi/2+color(red)(pi/2), color(white)(xx)(color(blue)4)1) rArr color(white)(xxxxxxxxx)(pi,4)`
Point `3. (pi+color(red)(pi/2), color(white)(xxx)(color(blue)4)0) rArr color(white)(axxxxxxxx)((3pi)/2,0)`
Point `4. ((3pi)/2+color(red)(pi/2), color(white)(ix)(color(blue)4)(-1)) rArr color(white)(xxxxxx)(2pi,-4)`
Point `5. (2pi+color(red)(pi/2), color(white)(xx)(color(blue)4)0) rArr color(white)(xxxxxxxxx)((5pi)/2,0)`

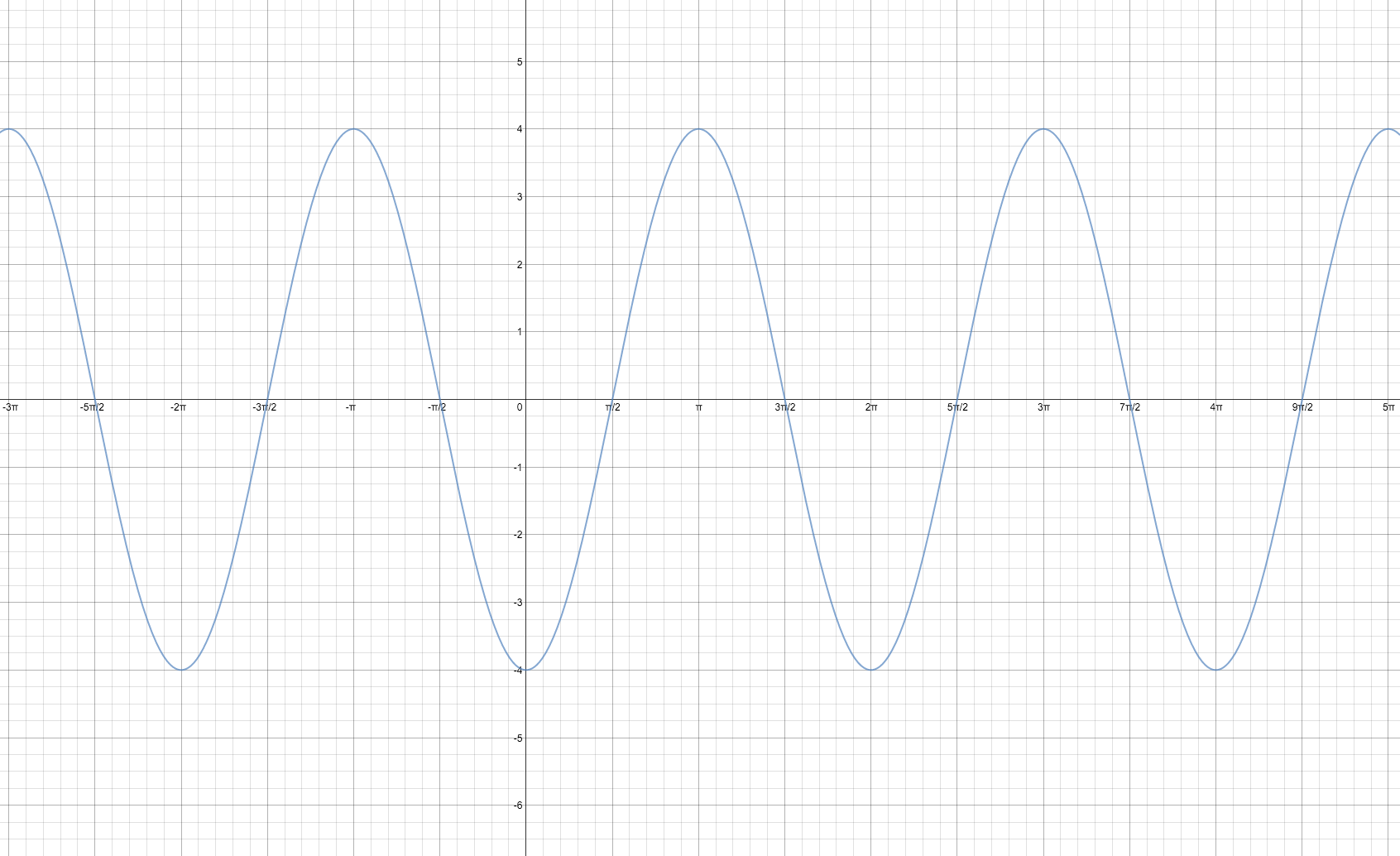
The transformed graph would look like:

![https://www.desmos.com/screenshot/6bf4rdat0g]()

Zoom in to check the five main points shown on the graph.