Question

A pyramid has a base in the shape of a rhombus and a peak directly above the base's center. The pyramid's height is `3`, its base has sides of length `2`, and its base has a corner with an angle of `(3 pi)/8`. What is the pyramid's surface area?

Answer 1

A = surface area `= 46.4` `units^2`

Explanation:

The surface area of a pyramid is

`A = "base area" xx 1/2 xx "base perimeter" xx "slant height"`

The base is the rhombus:

Area of a rhombus `= 1/2 pq`

where `p = BD and q = AC`

The internal angles of a quadrilateral `= 360^@ = 2pi = 32/16pi`

The diagonals of a rhombus are perpendicular.

The diagonals bisect the angles. This means if one corner angle is `3/8pi` then the half angle is `1/2 3/8pi = 3/16pi`

Use trigonometry to find the diagonal lengths:

`BE = DE = 2 sin 3/16 pi = 1.11114`; `BD = 2.22228`

`AE = CE = 2cos 3/16 pi = 1.66294`; `AC = 3.32588`

The base area is `1/2 (2.22228)(3.32588) = 3.6955` `units^2`

Base perimeter = `4(2) = 8`

To find the slant height use Pythagorean Theorem.


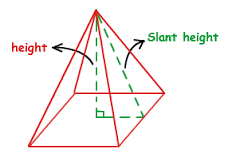
slant height = `sqrt (a^2 + height^2)`
where `a` = the length of the altitude, the perpendicular line from a side of the rhombus to the center of the rhombus.

`a = BE sin 5/16pi = .9239`.
Slant height = sqrt (.9239^2 + 3^2) = 3.139.

The Pyramid's surface area is

`A = 3.6955 (1/2) (8)(3.139) = 46.4` `units^2`