Question

Calculate the area a brick region? The length from the base of the rectangle to the top of the arc is called "Sagita".

Answer 1

Area of the brick structure`=8109-1/2 r^2 (theta – sin theta)`
Where `r and theta` as defined below.

Explanation:

Let `r` be the radius of the circle whose part is the segment under consideration.
To find the area of the segment we need to calculate 1. the area of the sector, 2. Area of the triangle and use the expression

`A_"Segment"=A_"Sector"- A_"Triangle"` .........(1)

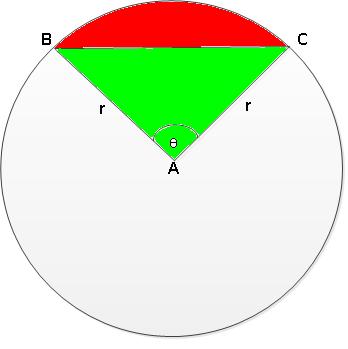
Given in the figure are chord `BC` of length `b` and `theta` angle subtended by the chord at the centre.
We can derive from (1) that

`A_"Segment" =1/2 r^2 theta – 1/2 r^2 sin(theta) =1/2 r^2 (theta – sin theta)`
-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-
1. `A_"Sector"`
Area of circle`=pir^2`, this area is enclosed by the angle `=2pi`.
Therefore area enclosed by angle `theta=(pir^2)/(2pi)xxtheta`
2. `A_"Triangle"`

In triangle `ABD`

`Sin(θ/2) = (BD)/(AB) or Sin(θ/2) = (b/2)/r or b = 2r Sin(θ/2)` ..(1)

`Cos(θ/2) = (AD)/(AB) or Cos(θ/2) = h/r or h = r Cos(θ/2)` ..(2)

Area of the Triangle `ABC = 1/2 b xx h`

Substitute the values of `b and h` from equation 1 and 2 we get

Area of Triangle `ABC = 1/2 [2r Sin(θ/2)] xx[r Cos(θ/2)]`
`= r^2 Sin(θ/2) Cos(θ/2)` ....(3)

Using trigonometric identity `2 SinA CosB = Sin(A+B)+Sin(A-B)`
and seeing that `A =B = θ/2`
Expressing `Sin(θ/2) Cos(θ/2)` in (3) we get

`Sin(θ/2) Cos(θ/2) = 1/2 [sin(θ/2+ θ/2) +sin(θ/2- θ/2)]`
since `sin(θ/2- θ/2) = sin (0) = 0`, we get

`Sin(θ/2) Cos(θ/2) = 1/2 sin(θ)` ..... (4)

Using (4), from equation (3) we get

Area of Triangle `ABC = 1/2 r^2 sin(θ)`
-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-..-.
From the figure in the main problem
`A_"Rectangle"=153xx53=8109m^2`
Given `e=21`, assuming that the sector is symmetrically placed
Chord `b=153-2xx21=111m`
Also `h=r-35` .....(5)
Area of the brick structure`=A_"Rectangle"-A_"Segment"`
Substituting given and calculated values
Area of the brick structure`=8109-1/2 r^2 (theta – sin theta)` ....(6)

Since numerical value of radius `r` is not available hence, general expression is as above.