How do you divide $\frac{- i + 1}{2 i + 10}$ $( -i+1) / (2i +10 )$ in trigonometric form?

Question

How do you divide $\frac{- i + 1}{2 i + 10}$ $( -i+1) / (2i +10 )$ in trigonometric form?

1 Answer

Impact of this question

1906 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-04-06T14:32:03

$\frac{- i + 1}{2 i + 10} = \frac{1}{2} (\frac{2}{13} - i \frac{3}{13})$ $(-i+1)/(2i+10) =1/2(2/13 - i3/13)$

Explanation:

A complex number $z$ $z$ is of the form

$z = a + b i$ $z=a+bi$

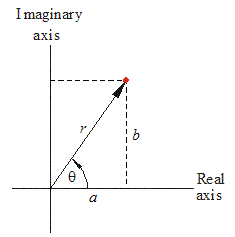
We define the Polar coordinates of $z$ $z$ to be $(r, θ)$ $(r,theta)$ , as seen in the image below.

![http://mathonweb.com/help_ebook/html/complex_2.htm]( useruploads.socratic.org )

From this diagram we get some more properties:

$r = \sqrt{a^{2} + b^{2}}$ $r=sqrt(a^2+b^2)$

$sin θ = \frac{b}{r} \Rightarrow b = r sin θ$ $sin theta = b/r => b=rsintheta$
$cos θ = \frac{a}{r} \Rightarrow a = r cos θ$ $costheta=a/r =>a=rcostheta$

If we substitute $b$ $b$ and $a$ $a$ into the definition of a complex number, we have

$z = r cos θ + i r sin θ = r (cos θ + i sin θ)$ $z=rcostheta+irsintheta = r(costheta+isintheta)$

Our trigonometric sum resembles $Euler's identity$ $color(red)("Euler's identity")$ :

$e^{i α} = cos α + i sin α$ $e^(icolor(red)alpha)=coscolor(red)alpha+isincolor(Red)(alpha$

Thus,

$z = r e^{i θ}$ $z=re^(itheta)$

In our case, it'd be easier to write them in this exponential form then transform it into trigonometric form.

Let $z_{1} = - i + 1$ $color(blue)(z_1 = -i+1$ and $z_{2} = 2 i + 10$ $color(blue)(z_2 = 2i+10$ .

We do not need to find $θ_{1}$ $theta_1$ and $θ_{2}$ $theta_2$ now, so we will let them as that.

$r_{1} = \sqrt{a_{1}^{2} + b_{1}^{2}} = \sqrt{1^{2} + {(- 1)}^{2}} = \sqrt{2}$ $r_1 = sqrt(a_1^2+b_1^2) = sqrt(1^2+(-1)^2) = sqrt2$
$r_{2} = \sqrt{a_{2}^{2} + b_{2}^{2}} = \sqrt{100 + 4} = \sqrt{104} = 2 \sqrt{26}$ $r_2 = sqrt(a_2^2+b_2^2)=sqrt(100+4)=sqrt(104)=2sqrt(26)$

$:. z_1/z_2=(r_1e^(itheta_1))/(r_2e^(itheta_2))$

$z_1/z_2 = sqrt2/(2sqrt26) * e^(i(theta_1-theta_2)$

$z_1/z_2 = 1/(2sqrt13) * e^(i(theta_1-theta_2)$

We can still apply Euler's identity to $e^(i(theta_1-theta_2))$ . We have:

$e^(i(theta_1-theta_2)) = cos(theta_1-theta_2)+isin(theta_1-theta_2)$

The $color(blue)("Difference formula")$ for cosine and sine is, as follows:

$cos(a-b)=cosacosb+sinasinb$
$sin(a-b) = sinacosb-cosasinb$

$cos(theta_1 - theta_2) = costheta_1costheta_2+sintheta_1sintheta_2$
$sin(theta_1-theta_2) = sintheta_1costheta_2-costheta_1sintheta_2$

From the properties we got earlier, we know:

$costheta_1 = 1/sqrt2$
$sintheta_1 = -1/sqrt2$

$costheta_2 = 5/sqrt26$
$sintheta_2=1/sqrt26$

After we calculate the values we needed, we reach this:

$cos(theta_1-theta_2) = 2/sqrt13$
$sin(theta_1-theta_2)= -3/sqrt13$

Finally, we get:

$z_1/z_2 = 1/(2sqrt13) (2/sqrt13 -i3/sqrt13)$

$z_1/z_2 = 1/2(2/13 - i3/13)$

$:.$

$(-i+1)/(2i+10) =1/2(2/13 - i3/13)$

Science

Math

Humanities

... and beyond

How do you divide $\frac{- i + 1}{2 i + 10}$ $( -i+1) / (2i +10 )$ in trigonometric form?

1 Answer

Explanation:

Related questions

Impact of this question

Science

Math

Humanities

... and beyond

How do you divide ( -i+1) / (2i +10 )−i+12i+10( -i+1) / (2i +10 ) in trigonometric form?

1 Answer

Explanation:

Related questions

Impact of this question

How do you divide $\frac{- i + 1}{2 i + 10}$ $( -i+1) / (2i +10 )$ in trigonometric form?