What is the area of a hexagon with an apothem of 9?
1 Answer
Explanation:
The apothem is the length from the center of a regular polygon to the midpoint of one of its sides. It is perpendicular (
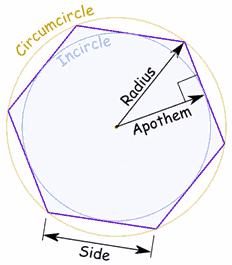
You can use the apothem as the height for the whole triangle:
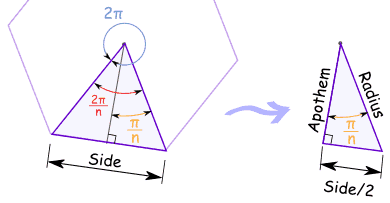
To find the area of the whole triangle, we first need to find the length of the base, since the base length is unknown.
To find the base length, we can use the formula:
#base=apothem*2*tan(pi/n)#
where:
#base=apothem*2*tan(pi/n)#
#base=9*2*tan(pi/6)#
#base=18*tan(pi/6)#
#base=18*sqrt(3)/3#
#base=(18sqrt(3))/3#
#base=(color(red)cancelcolor(black)(18)^6sqrt(3))/color(red)cancelcolor(black)(3)#
#base=6sqrt(3)#
To find the area of the hexagon, find the area of the whole triangle and multiply the value by
#Area=((base*apothem)/2)*6#
#Area=((base*apothem)/color(red)cancelcolor(black)(2))*color(red)cancelcolor(black)(12)^3#
#Area=base*apothem*3#
#Area=6sqrt(3)*9*3#
#Area=54sqrt(3)*3#
#Area=162sqrt(3)#

