What is the area of a regular hexagon with an apothem of 6m in length?
1 Answer
Explanation:
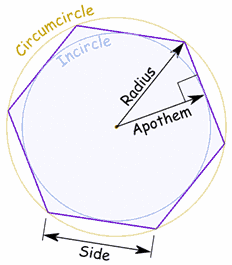
With reference to the regular hexagon, from the image above we can see that it is formed by six triangles whose sides are two circle's radii and the hexagon's side. The angle of each of these triangles' vertex that is in the circle center is equal to
The apothem divides equally each one of the equilateral triangles in two right triangles whose sides are circle's radius, apothem and half of the hexagon's side. Since the apothem forms a right angle with the hexagon's side and since the hexagon's side forms
As already mentioned the area of the regular hexagon is formed by the area of 6 equilateral triangles (for each of these triangle's the base is a hexagon's side and the apothem functions as height) or:
=>

