What`s the surface area formula for a rectangular pyramid?
1 Answer
Explanation:
![http://4.bp.blogspot.com]()
The surface area will be the sum of the rectangular base and the
Area of the Rectangular Base
The base simply has an area of
#=>lw#
Area of Front and Back Triangles
The area of a triangle is found through the formula
Here, the base is
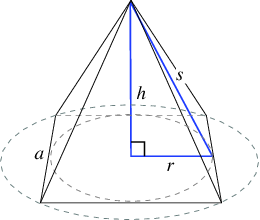
The slant height can be found through solving for the hypotenuse of a right triangle on the interior of the pyramid.
The two bases of the triangle will be the height of the pyramid,
This is the height of the triangular face. Thus, the area of front triangle is
#=>lsqrt(h^2+(w/2)^2)#
Area of the Side Triangles
The side triangles' area can be found in a way very similar to that of the front and back triangles, except for that their slant height is
#=>wsqrt(h^2+(l/2)^2)#
Total Surface Area
Simply add all of the areas of the faces.
#"SA"=lw+lsqrt(h^2+(w/2)^2)+wsqrt(h^2+(l/2)^2)#
This is not a formula you should ever attempt to memorize. Rather, this an exercise of truly understanding the geometry of the triangular prism (as well as a bit of algebra).

