Make the internet a better place to learn

#l = 8, b = 2, theta = (5pi)/12, h = 9#

#"To find the Total Surface Area T S A"#

#"Area of parallelogram base " A_B = l b sin theta#

#A_B = 8 * 2 * sin ((5pi)/12) = 15.45#

#S_1 = sqrt(h^2 + (b/2)^2) = sqrt(9^2 + 1^2) = 9.06#

#S_2 = sqrt(h^2 + (l/2)^2) = sqrt(9^2 + 4^2) = 10.82#

#"Lateral Surface Area " A_L = 2 * ((1/2) l * S_1 + (1/2) b * S_2#

#A_L = (cancel2 * cancel(1/2)) * (l * S_1 + b * S_2) = (8 * 9.06 + 2 * 10.82)#

#A_L = 94.12#

#"Total Surface Area " A_T = A_B + A_L = 15.45 + 94.12 = 109.57#

Without loss of generality, one of the vertices is at #(0, 0)#.

Let the vertex anticlockwise from #(0, 0)# be #(m, n)# for some integers #m# and #n#.

The midpoint of the corresponding side is #(m/2, n/2)#

The line through #(0, 0)# and #(m, n)# has slope #n/m#, so any perpendicular to this side has slope #-m/n#.

The third vertex of the triangle lies on the line through the midpoint #(m/2, n/2)# with slope #(-m/n)#.

In fact it will lie at the point:

#(m/2, n/2) + sqrt(3)/2 (-n, m) = ((m-sqrt(3)n)/2, (n+sqrt(3)m)/2)#

since the height of an equilateral triangle is #sin 60^@ = sqrt(3)/2# times the length of one of the sides.

So we require #(m-sqrt(3)n)/2# to be an integer and #(n+sqrt(3)m)/2# to be an integer.

Since #sqrt(3)# is irrational, this would imply that #n=0# and #m=0#, hence there is no such triangle.

The trapezoid described is somewhat as the figure below:

The formula of the area of the triangle is
#S_(triangle AED)=(base*height)/2#

Since AF is perpendicular to the triangle's side DE, and AF=BC=12, we have:
#S_(triangle AED)=(DE*AF)/2=(4*12)/2=24#

This is Geometry, so lets look at at a picture of what we are dealing with:

#A_("circle") = pi*r^2color(white)("XXX")rarrcolor(white)("XXX")r=sqrt(A/pi)#

We are told
#color(white)("XXX")A=152 "cm"^2#
and to use
#color(white)("XXX")pi = 22/7#

#rArr r= 7# (after some minor arithmetic)

If #s# is the length of one side of the equilateral triangle and #t# is half of #s#

#color(white)("XXX")t=r*cos(60^@)#

#color(white)("XXXx")=7*sqrt(3)/2#

and
#color(white)("XXX")s=2t = 7*sqrt(3)#

#color(white)("XXXx")=12.11# (since we are told to use #sqrt(3)=1.73#)

Perimeter #=3s#

#color(white)("XXXXXX")=3 xx 12.11 = 36.33#

The area of any triangle is given by #1/2*b*h# where #b# is the base and #h# is the hieght.
Therefore the area here is #1/2*5*4 = 10#

The above triangle is a right angled isosceles triangle , with #BC = AC#

The length of the leg given #=5sqrt2cm# (assuming units to be in cm)

So, #BC = AC = 5sqrt2 cm#

The value of the hypotenuse #AB# can be calculated using the Pythagoras theorem:

#(AB)^2 = (BC)^2 +(AC)^2#

#(AB)^2 = (5sqrt2)^2 +(5sqrt2)^2#

#(AB)^2 = 50 +50#

#(AB)^2 = 100#

#(AB) = sqrt100#

#AB = 10 cm#

In a regular polygon each interior angle can be obtained in this way:
#alpha=180^@-360^@/n#

From the conditions of the problem:
#136^@ < alpha<142^@#

That's the conjugation of this two inequations:
#136^@ < alpha# and #alpha<142^@#

Resolving the first inequation
#136^@<180^@-360^@/n#
#136^@<(180^@*n-360^@)/n# => #136^@*n<180^@.n-360^@# => #44^@.n>360^@# => #n>8.18#

Resolving the second inequation
#180^@-360^@/n<142^@#
#180^@*n-360^@<142^@*n# => #38^@.n<360^@# => #n<9.47#

Conjugating the two inequations
#8.18 < n<9.47#

Since #n in NN#, its only value that satisfies the inequation is #n=9#

By the way
#alpha=180^@-360^@/9=180^@-40^@# => #alpha=140^@#

Consider Figs. 1 and 2

Figure 1 shows two circles (with centers #C1# and #C2# and radii #r_1# and #r_2#) that intercept each other in points A and B.

The area of interest is encompassed by arcs ADB and AEB.

In such a problem, most probably #r_1# and #r_2# are informed or aren't hard to find. This means that we can easily know the area of both the circles (as #pi*r_1^2# and #pi*r_2^2#).

We only need one more information to determine the area of the region ADBE: the proportion of any of the areas of circular sector to the total area of its circle or the angle of the circular sector (#alpha# or #beta#) or the length of the chord AB or even the coordinates of the center points #C1# and #C2#.

If we have the coordinates of the center points C1 and C2 as well as the radii #r_1# and #r_2#, we can obtain the circles' equations of whose conjugation we can obtain points A and B and therefore the length of the cord AB.

If we get the chord AB (called "x" in Figure 2 ) we can obtain #alpha# and #beta# in this way:
#tan (alpha/2)=(x/2)/r_1#
#tan (beta/2)=(x/2)/r_2#

Knowing #alpha# and #beta# we can determine the area of the circular sectors:
#S_("circular sector 1")=(alpha/360^@)*S_(circ_ 1)=(alpha/360^@)*pi*r_1^2#
#S_("circular sector 2")=(alpha/360^@)*S_(circ_ 2)=(alpha/360^@)*pi*r_2^2#

Next we can easily find #h_1# (height of #triangle_(ABC1)# in circle 1) and #h_2# (height of #triangle_(ABC2)# in circle 2).
Then with the chord AB (#=x#) as base and #h_1# or #h_2# as height we find the area of triangles ABC1 and ABC2.

Next we need just to subtract from each circular sector the area of its triangle.
Finally, we sum the results of the aforementioned subtractions obtaining the area of interest. Job done!

OR we could integrate the area between the equations of the two circles from the point A (#x_A, y_A#) to the point B (#x_B, y_B#).

To ease the comprehension of the problem refer to the figure below:

If the sides BC and AD are extended the #triangle_(ABF)#, equilateral, is formed.

First, in addition to the angles informed it was possible to determine other interior angles of the triangles ABC and ABD, as shown in the figure.

Then using the Law of Sines on these triangles:

• #triangle_(ABC)#

#"AB"/sin (120^@-alpha)="BC"/sin alpha="AC"/sin 60^@#

• #triangle_(ABD)#

#"AB"/sin (60^@+alpha)="AD"/sin (60^@-alpha)="BD"/sin 60^@#

To focus on viable hypotheses I suggest to begin trying to prove a specific case.
For instance #AB =5# and #alpha = 15^@#:

From #triangle_(ABC) -> 5/(sin 105^@)="BC"/sin 15^@# => # BC = 5*sin 15^@/sin 105^@#

From #triangle_(ABD) -> 5/(sin 75^@)="AD"/sin 45^@# => # AD=5*sin 45^@/sin 75^@#

Note that #sin 75^@=sin 105# because #75^@# and #105^@# are supplementary angles and sines of angles of the first and second quadrants are positive.

Finally,

#AD+BC=5*(sin 15^@+sin 45^@)/(sin 75^@)=5*1=AB#

So in this case hypothesis (C) is true (I tried the others and verified that they are false.)

Now for the general proof of the hypothesis (C), following the same steps that worked for the specific proof:

From #triangle_(ABC) -> "AB"/sin (120^@-alpha)="BC"/sin alpha#

Observation:

#sin (120^@-alpha)=sin (180^@-(120^@-alpha))=sin(60^@+alpha)#

#=>"AB"/sin (60^@+alpha)="BC"/sin alpha => "BC"="AB"*sin alpha/sin (60^@+alpha)#

Therefore,

# "BC" ="AB" * (sin alpha)/((sqrt(3)/2)*cos alpha+(1/2)*sin alpha)#

From #triangle_(ABD) -> "AB"/sin (60^@+alpha)="AD"/sin(60^@-alpha)#

This will get you

#AD="AB"*sin(60^@-alpha)/sin (60^@+alpha)#

#=AB((sqrt(3)/2)*cos alpha-(1/2)*sin alpha)/((sqrt(3)/2)*cos alpha+(1/2)*sin alpha)#

Finally,

#BC+AD="AB"(sin alpha+(sqrt(3)/2)*cos alpha-(1/2)*sin alpha)/((sqrt(3)/2)*cos alpha+(1/2)*sin alpha)#

#BC + AD ="AB" * 1#

Therefore,

#AB=BC+AD# and the hypothesis (C) is true.**

For a rectangular prism with sides #w,l,h#, the surface area is

#"SA"=2(wl+lh+hw)#

This occurs since there are two pairs of three different faces on every rectangular prism.

Each pair of faces is a different rectangle using two of the the three dimensions of the prism as its own side.

One side is just #wl#, another is just #lh#, and the other #hw#. Since there are two of each, that is reflected in the formula by the multiplication by #2#.

This could also be imagined as a series of flattened-out rectangles:

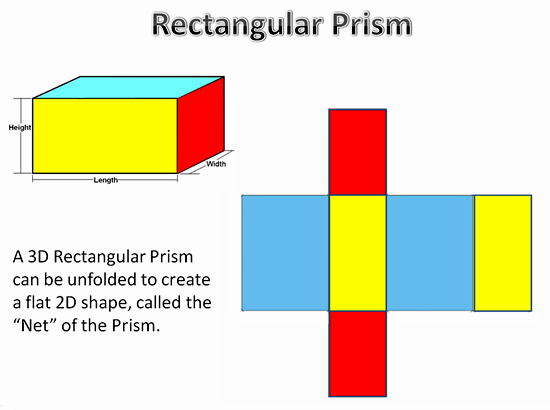
The blue rectangles are #2*wl#.

The yellow rectangles are #2*lh#.

The red rectangles are #2*hw#.

Again, the surface area would be

#"SA"=2wl+2lh+2hw#

#=2(wl+lh+hw)#