A circle's center is at #(8 ,1 )# and it passes through #(2 ,5 )#. What is the length of an arc covering #( pi ) /6 # radians on the circle?

1 Answer
sankarankalyanam
Apr 18, 2018

#color(indigo)("Arc Length " s = r * theta = 1.2 pi = 3.77 " units"#

Explanation:

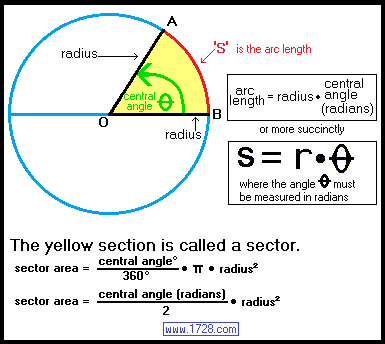
![http://www.1728.org/http://radians.htm](https://useruploads.socratic.org/DXaqqwRrQOSGOu4GMsPq_arc%20length.jpg)

Given : #"centre (8,1), Point on circumference (2,5) ", theta = pi/6#

#" Radius " r = bar (OA) = sqrt ((8-2)^2 + (1-5)^2)#

#r = sqrt(6^2 + 4^2) = sqrt 52 = 7.2#

#color(indigo)("Arc Length " s = r * theta = 7.2 * (pi/6) = 1.2 pi = 3.77 " units"#

Related questions
See all questions in Circle Arcs and Sectors
Impact of this question
1938 views around the world
You can reuse this answer
Creative Commons License